上海崇明区2017-2018学年第二学期初一数学期中卷
1、选择题(本大题共6小题,共18.0分)
C. 无限小数都是无理数 D. 实数包含有理数和无理数
B. 连接直线外一点与直线上各点的所有线段中,垂线段最短
C. 假如两条直线被第三条直线所截,那样内错角相等
D. 经过一点有且只有一条直线与已知直线平行
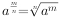 如图:与∠C互为同旁内角的角有()
如图:与∠C互为同旁内角的角有() B. 2个
C. 3个
D. 4个.
|
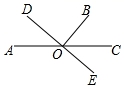 如图:若∠BOC=52°,BO⊥DE,垂足为O,则∠AOD=______度.
如图:若∠BOC=52°,BO⊥DE,垂足为O,则∠AOD=______度.
|
 如图:DE∥BC,CD是∠ACB的平分线,∠ACB=70°,则∠EDC=______度.
如图:DE∥BC,CD是∠ACB的平分线,∠ACB=70°,则∠EDC=______度.
|
 如图:l1∥l2,∠1=65°,∠2=48°,那样∠3=______度.
如图:l1∥l2,∠1=65°,∠2=48°,那样∠3=______度.
|
 如图:AD∥BC,BD平分∠ABC,∠A:∠ABD=5:2,则∠ABD=______度.
如图:AD∥BC,BD平分∠ABC,∠A:∠ABD=5:2,则∠ABD=______度.
|
3、计算题(本大题共1小题,共6.0分)
(2)
(3)
(4)
(5)
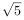 如图,已知A、B、D在一直线上AE∥BC,AE平分∠DAC,请填写∠B=∠C的原因
如图,已知A、B、D在一直线上AE∥BC,AE平分∠DAC,请填写∠B=∠C的原因解:由于AE平分∠DAC______
所以∠1=∠2______
由于AE∥BC______
所以∠1=∠B______
∠2=∠C______
所以∠B=∠C______
|
 如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的原因.
如图所示,已知AD⊥BC,垂足为点D,EF⊥BC,垂足为点F,∠1+∠2=180°.请填写∠CGD=∠CAB的原因.解:由于AD⊥BC,EF⊥BC(______)
所以∠ADC=90°,∠EFD=90°(______)
得∠ADC=∠EFD(等量代换),
所以AD∥EF(______)
得∠2+∠3=180°(______)
由∠1+∠2=180°(______)
得∠1=∠3(______)
所以DG∥AB(______)
所以∠CGD=∠CAB(______)
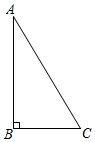 在△ABC中,∠B=90°.
在△ABC中,∠B=90°.(1)画线段AC的垂直平分线MN,交AC于点M,交AB于点N.
(2)过点M作ME∥BC交AB于点E.
(3)直线BC与直线ME之间的距离是线段______的长.
|
 如图,已知AB∥CD,∠1=∠C.试说明EF∥CG.
如图,已知AB∥CD,∠1=∠C.试说明EF∥CG.
|
 如图所示,已知∠BAP+∠APD=180°,∠1=∠2,请说明AE∥PF的原因.
如图所示,已知∠BAP+∠APD=180°,∠1=∠2,请说明AE∥PF的原因.
|
(1)图a中,∠AEG=______°;
(2)图a中,∠BMG=______°;
(3)图b中,∠EFN=______°.
 |
【分析】
B、
C、-
D、
故选:B.
先把能化简的数化简,然后依据无理数的概念逐一判断即可得.
本题主要考查无理数的概念,依据无理数的概念逐一进行判断是解决本题的重点,是简单题.
【分析】
有理数包含有限小数与无限循环小数,∴答案B错误;
无限小数中包含无限循环小数,是有理数,∴答案C错误;
依据实数概念,有理数和无理数统称为实数,∴答案D正确;
故选:D.
依据实数的分类,与有理数与无理数的概念即可判断以上选项.
本题考查的是实数的概念与分类,重点要不同有理数与无理数的定义,特别应该注意无限小数的范围.
【分析】
B、
C、-
D、
故选:B.
依据二次根式的运算法则依次计算即可求解.
本题考查了学生的运算能力,解题的重点是熟练运用二次根式的性质和运算法则,本题是基础题型.
【分析】
B、连接直线外一点与直线上各点的所有线段中,垂线段最短,正确;
C、假如两条平行直线被第三条直线所截,那样内错角相等,故错误;
D、经过直线外一点有且只有一条直线与已知直线平行,故错误,
故选:B.
借助对顶角的性质、垂线的性质、平行线的性质及平行公理分别判断后即可确定正确的选项.
本题考查了对顶角的性质、垂线的性质、平行线的性质及平行公理等常识,解题的重点是知道有关的定理及概念,困难程度不大.
【分析】
故选:C.
依据两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则如此一对角叫做同旁内角进行解答即可.
本题考查了同旁内角的概念.注意在截线的同旁找同旁内角.要结合图形,熟记同旁内角的地方特征.
【分析】
a>0,b<0,|a|<|b|,
∴|a+b|=-a-b,|a-b|=a-b,
∴原式=|a-b|-|a+b|=a-b+a+b=2a,
故选:A.
依据数轴,先确定a、b的正负,即a>0,b<0,|a|<|b|,得出|a+b|=-a-b,|a-b|=a-b,即可得出结果.
此题主要考查了绝对值的运算和二次根式的运算,先确定绝对值符号中代数式的正负再去绝对值符号,借用数轴化简含有绝对值的式子,困难程度适中.
【分析】
∴25的平方根±5.
故答案为:±5.
依据平方根的概念,结合(±5)2=25即可得出答案.
本题考查了平方根的常识,是基础题,解答本题的重点是学会平方根的概念,注意一个正数的平方根有两个且互为相反数.
【分析】
得
故答案为
依据分数指数幂公式
本题考查了分数指数幂,正确理解分数指数幂的意思是解题的重点.
【分析】
∴x=
故答案为:
依据负整数指数幂的运算办法,求出x的值是多少即可.
此题主要考查了负整数指数幂的运算,要熟练学会,解答此题的重点是要明确:①a-p=(a≠0,p为正整数);②计算负整数指数幂时,必须要依据负整数指数幂的意义计算;③当底数是分数时,只须把分子、分母颠倒,负指数就可变为正指数.
【分析】
故答案为:百,3.
用科学记数法a×10n(1≤a<10,n是正整数)表示的数的有效数字应该由首数a来确定,首数a中的数字就是有效数字,据此解答即可.
本题考查了近似数的有效数字,正确理解有效数字的意义是解题的重点.
【分析】
故答案为:
直接借助算术平方根的概念计算得出答案.
此题主要考查了算术平方根,正确把握有关概念是解题重点.
【分析】
∴π<
故答案为:<.
分别看出π、
此题主要考查了实数大小比较的办法,要熟练学会,解答此题的重点是分别看出π、
【分析】
AB=|3
=|3
=5
故答案为5
依据数轴上两点间的距离公式即可得AB的长度.
本题考查的是数轴上两点间的距离,依据两点间距离公式即可求解,重点是关系到二次根式的运算.
【分析】
答:另一个角为115°,
故答案为:
115.
依据邻补角的概念即可得到结论.
本题考查了对顶角、邻补角,熟记概念是解题的重点.
【分析】
∴∠AOD=180°-52°-90°=38°.
故答案为:38.
需先依据已知条件和所给的图形,列出所需要的式子,即可求出答案.
本题主要考查了垂线,在解题时要依据已知有条件,再结合图形列出式子是本题的重点.
【分析】
∴∠EDC=∠DCB,
∵CD是∠ACB的平分线,
∴∠ECD=∠DCB,
∴∠EDC=∠ECD,
∵∠ACB=70°,
∴∠EDC=∠ECD=35°.
故答案为:35.
借助平行线的性质得出∠EDC=∠DCB,借助角平分线的性质得出∠EDC=∠ECD进而求出即可.
此题主要考查了平行线的性质与角平分线的性质等常识,依据已知得出∠EDC=∠ECD是解题重点.
【分析】

∵l1∥l2,
∴∠4=180°-∠2-∠1=180°-65°-48°=67°,
∴∠3=∠4=67°,
故答案为67.
借助平行线的性质求出∠4即可解决问题.
本题考查平行线的性质,解题的重点是熟练学会入门知识,是中考常考试试题型.
【分析】
∠A+∠ABC=180°
∵BD平分∠ABC,
∴∠ABD=∠DBC,
设∠ABD=2x,则∠A=5x,
∴9x=180°,
∴x=20°,
∴ABD=2x=40°
故答案为40.
设∠ABD=2x,则∠A=5x构建方程即可解决问题.
本题考查平行线的性质,角平分线的概念等常识,解题的重点是掌握借助参数构建方程解决问题.
=
(2)原式=
=5×3
=90
(3)原式=[(2-
=(4-3)2
=1;
(4)原式=
=
=22
=4;
(5)原式=
=
【分析】
(1)依据二次根式的加减运算法则即可求出答案.
(2)依据二次根式的乘除运算法则即可求出答案.
(3)依据平方差公式即可求出答案.
(4)依据幂的运算法则即可求出答案.
(5)依据分数指数幂的意义与负整数指数幂的意义即可求出答案.
本题考查实数运算,解题的重点是熟练运用实数的运算法则,本题是基础题型.
【分析】
所以∠1=∠2 (角平分线的概念)
由于AE∥BC (已知)
所以∠1=∠B (两直线平行同位角相等)
∠2=∠C (两直线平行内错角相等)
所以∠B=∠C (等量代换)
故答案为:已知,角平分线的概念,已知,两直线平行同位角相等,两直线平行内错角相等,等量代换.
借助平行线的性质,角平分线的概念即可解决问题.
本题考查平行线的性质,角平分线的概念等常识,解题的重点是灵活运用所学常识解决问题,是中考常考试试题型.
【分析】
∴∠ADC=90°,∠EFC=90°(垂直概念),
∴∠ADC=∠EFD,
∴AD∥EF(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠1+∠2=180°(已知),
∴∠1=∠3(同角的补角相等),
∴DG∥AB(内错角相等,两直线平行),
∴∠CGD=∠CAB(两直线平行,同位角相等).
故答案为:已知,垂直概念,同位角相等,两直线平行,两直线平行,同旁内角互补,已知,同角的补角相等,内错角相等,两直线平行,两直线平行,同位角相等.
求出AD∥EF,依据平行线的性质得出∠2+∠3=180°,求出∠1=∠3,依据平行线的断定得出DG∥AB,依据平行线的性质得出∠CGD=∠CAB即可.
本题考查了平行线的性质和断定,垂直概念,补角概念的应用,能综合运用定理进行推理是解此题的重点,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.
【分析】

(2)如图所示,ME即为所求;
(3)直线BC与直线ME之间的距离是线段BE的长,
故答案为:BE.
(1)依据线段中垂线的尺规作图可得;
(2)依据过直线外一点作已知直线的尺规作图作ME⊥AB,即可得;
(3)由直线间的距离的定义求解可得.
本题主要考查作图-复杂作图,解题的重点是学会线段中垂线和过直线外一点作已知直线的尺规作图及平行线间的距离.
∴∠2=∠C,
∵∠1=∠C,
∴∠1=∠2,
∴EF∥CG.
【分析】
依据平行线的断定和性质即可得到结论.
本题考查了平行线的断定和性质,熟练学会平行线的断定和性质是解题的重点.
 证明:如图所示,∵∠BAP+∠APD=180°,
证明:如图所示,∵∠BAP+∠APD=180°,∴PD∥AB,
∴∠下载成本=∠CAB,
又∵∠1=∠2,
∴∠下载成本-∠2=∠CAB-∠1,即∠CPF=∠CAE,
∴AE∥PF.
【分析】
先断定PD∥AB,再依据平行线的性质,即可得到∠下载成本=∠CAB,再依据等式性质即可得出∠CPF=∠CAE,进而断定AE∥PF.
本题考查了平行线的断定定理,正确辨别“三线八角”中的同位角、内错角、同旁内角是正确答卷的重点,不可以遇见相等或互补关系的角就误觉得具备平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
【分析】
∴∠HFM=180°-140°=40°.
∴∠EFC=70°+40°=110°.
∵AD∥BC,
∴∠DEF=180°-110°=70°,
∴∠GEF=∠DEF=70°,
∴∠AEG=180°-70°-70°=40°.
故答案为:40;

(2)∵由(1)知,∠HFM=40°,∠H=∠C=90°,
∴∠HMF=90°-40°=50°.
∵∠HMF与∠BMG是对顶角,
∴∠BMG=∠HMF=50°.
故答案为:50;
(3)∵△MNF由△MHF翻折而成,
∴∠MFN=∠HFM=40°,
∵∠BFE=70°,
∴∠EFN=∠BFE-∠MFN=70°-40°=30°.
故答案为:30.
(1)先依据∠BFE=70°求出∠HFM的度数,进可得出∠EFC的度数,依据平行线的性质求出∠DEF的度数,由平角的概念即可得出结论;
(2)由(1)知,∠HFM=40°,再由翻折变换的性质得出∠H=∠C=90°,由三角形内角和定理得出∠HMF的度数,依据对顶角相等即可得出结论;
(3)先依据图形翻折变换的性质得出∠MFN=∠HFM=40°,再由∠BFE=70°即可得出结论.
本题考查的是平行线的性质,用到的要点为:两直线平行,同旁内角互补.







