上海浦东新区川沙中学南校初二(下)第二次月考数学试题(五四学制)
1、选择题:(每题3分,共18分)
1.(3分)一个多边形的每个外角等于72°,这个多边形是()
A.正三角形 B.正方形 C.正五边形 D.正六边形
2![]() .(3分)已知:①平行四边形 ②矩形 ③菱形 ④等腰三角形 ⑤等腰梯形.这5种图形中,既是中心对称图形,又是轴对称图形的有()
.(3分)已知:①平行四边形 ②矩形 ③菱形 ④等腰三角形 ⑤等腰梯形.这5种图形中,既是中心对称图形,又是轴对称图形的有()
A.2种 B.3种 C.4种 D.5种
3.(3分)下列命题中,假命题是()
A.两条对角线互相平分的四边形是平行四边形
B.两条对角线互相垂直的平行四边形是菱形
C.两条对角线相等的平行四边形是矩形
D.两条对角线互相垂直且相等的四边形是正方形
4.(3分)如图,梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A![]() =100°,则∠C=()
=100°,则∠C=()
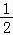
A.80° B.70° C.75° D.60°
5.(3分)顺次连结等腰梯形四边中点所得到的四边形的形状是()
A.平行四边形 B.正方形 C.菱形 D.矩形
6.(3分)在矩形ABCD中,|AB|=![]() ,|BC|=1,则向量(AB+BC+AC)的长度为()
,|BC|=1,则向量(AB+BC+AC)的长度为()
A.4 B.![]() C.
C.![]() 或
或![]()
![]() D.
D.![]()
2、填空题:(每题3分,共36分)
7.(3分)已知平行四边形一组对角的和等于270°,那样在这个平行四边形中较小的一个内角等于__________度.
8.(3分)梯形的下底长为12cm,中位线长为8cm,则它的上底长为__________cm.
9.(3分)向量:![]() ﹣
﹣![]() +
+![]() =__________.
=__________.
10.(3分)有一个内角等于120°的菱形,周长为12,则较短的对角线长为__________.
11.(3分)如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为__________.

12.(3分)正方形的对角线长是![]() cm,则正方形的周长是__________,面积是__________.[来源:学.科.网Z.X.X.K]
cm,则正方形的周长是__________,面积是__________.[来源:学.科.网Z.X.X.K]
13.(3分)假如等腰梯形的腰长是5,上、下底的长分别为![]() 3、9,那样它的面积为__________.
3、9,那样它的面积为__________.
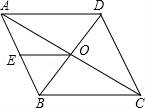
14.(3分)如图,在矩形ABCD中,假如AB=![]() BC,BE=BC,那样∠DCE=__________度.
BC,BE=BC,那样∠DCE=__________度.

15.(3分)假如一个平行四边形一个内角的平分线分它的一边为1:2的两部分,那样称如此的平行四边形为“协调平行四边形”,称该边为“协调边”.当“协调边”为3时,它的周长为__________.
16.(3分)如图,菱形ABCD中,点E是AB的中点.已知AC=8cm,BD=6cm,则OE=__________.
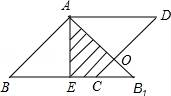
17.(3分)已知正方形ABCD的边长为6,点E是边BC的中点.联接AC、DE相交于点F,M、N分别是AC、DE的中点,则MN的长是__________.
18.(3分)如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是__________.

3、解答卷:(共46分)
19.(8分)如图已知:矩形ABCD,对角线AC、BD相交于点O.
(1)借助图中的向量表示:![]() +
+![]() =__________;
=__________;
(2)借助图中的向量表示:![]() ﹣
﹣![]() =__________;
=__________;
(3)假如|![]() |=5,|
|=5,|![]() |=5,则|
|=5,则|![]() |=__________.
|=__________.

20.(10分)如图,菱形ABCD的对角线AC与BD相交于点O,已知AB=13cm,AC=24cm.
(1)求:菱形ABCD的面积;
(2)如过点D作DE⊥BC,垂足为E,求DE的长.
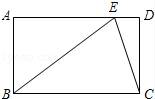
21.(6分)如图,点O是平行四边形ABCD的对角线AC与BD的交点,四边形OCDE是平行四边形.
求证:OE与AD互相平分.
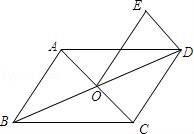
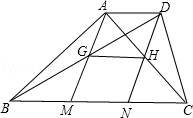
22.(10分)如图,梯形ABCD中,AD∥BC,BC=3![]() AD,M、N为底边BC的三等分点,连接AM,DN.
AD,M、N为底边BC的三等分点,连接AM,DN.
(1)求证:四边形AMND是平行四边形;
(2)连接BD、AC,AM与对角线BD交于点G,DN与对角线AC交于点H,且AC⊥BD.试判断四边形AGHD的形状,并证明你的结论.
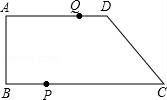
23.(12分)在梯形ABCD中,∠ABC=90°,AD∥BC,BC>AD,AB=8cm,BC=18cm,CD=10cm,点P从点B开始沿BC边向终点C以每秒3cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度移动,设运动时间为t秒.
(1)求四边形ABPQ为矩形时t的值;
(2)若题设中的“BC=18cm”改变为“BC=kcm”,其它条件都不变,要使四边形PCDQ是等腰梯形,求t与k的函数关系式,并写出k的取值范围;
(3)在移动的过程中,是不是存在t使P、Q两点的距离为10cm?若存在求t的值,若没有请说明理由.
上海浦东新区川沙中学南校初二(下)第二次月考数学试题(五四学制)
参考答案与考试试题分析
1、选择题:(每题3分,共18分)
1.(3分)一个多边形的每个外角等于72°,这个多边形是()
A.正三角形 B.正方形 C.正五边形 D.正六边形
【解答】解:360°÷72°=5,则多边形的边数是5.
故选:C.
2.(3分)已知:①平行四边形 ②矩形 ③菱形 ④等腰三角形 ⑤等腰梯形.这5种图形中,既是中心对称图形,又是轴对称图形的有()
A.2种 B.3种 C.4种 D.5种
【解答】解:①平行四边形,是中心对称图形,不是轴对称图形;
②矩形,既是中心对称图形,又是轴对称图形;
③菱形,既是中心对称图形,又是轴对称图形;
④等腰三角形,不是中心对称图形,是轴对称图形;
⑤等腰梯形,不是中心对称图形,是轴对称图形;
综上所述,既是中心对称图形,又是轴对称图形的有矩形和菱形共2种.
故选:A.
3.(3分)下列命题中,假命题是()
A.两条对角线互相平分的四边形是平行四边形
B.两![]() 条对角线互相垂直的平行四边形是菱形
条对角线互相垂直的平行四边形是菱形
C.两条对角线相等的平行四边形是矩形
D.两条对角线互相垂直且相等的四边形是正方形
【解答】解:A、两条对角线互相平分的四边形是平行四边![]() 形,正确,是真命题;
形,正确,是真命题;
B、两条对角线互相垂直的平行四边形是菱形,正确,是真命题;
C、两条对角线相等的平行四边形是矩形,正确,是真命题;
D、两条对角线互相垂直且相等的平行四边形是正方形,错误,是假命题;
故选:D.
4.(3分)如图,梯形ABCD中,AD∥BC,AD=AB,BC=BD,∠A=100°,则∠C=()
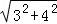
A.80° B.70° C.75° D.60°
【解答】解:∵AB=AD
∴∠ADB=![]() (180°﹣∠A)=40°
(180°﹣∠A)=40°
又∵AD∥BC
∴∠DBC=∠ADB=40°
又∵BC=BD
∴∠C=![]() (180°﹣∠DBC)=
(180°﹣∠DBC)=![]() (180°﹣40°)=70°.
(180°﹣40°)=70°.
故选:B.
5.(3分)顺次连结等腰梯形四边中点所得到的四边形的形状是()
A.平行四边形 B.正方形 C.菱形 D.矩形
【解答】解:如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是各边的中点,
求证:四边形EFGH是菱形.
证明:连接AC、BD.
∵E、F分别是AB、BC的中点,
∴EF=![]() AC.
AC.
同理FG=![]() BD,GH=
BD,GH=![]() AC,EH=
AC,EH=![]() BD,
BD,
又∵四边形ABCD是等腰梯形,
∴AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
故选:C.
6.(3分)在矩形ABCD中,|AB|=![]() ,|BC|=1,则向量(AB+BC+AC)的长度为()
,|BC|=1,则向量(AB+BC+AC)的长度为()
A.4 B.![]() C.
C.![]() 或
或![]() D.
D.![]()
【解答】解:∵在矩形ABCD中,|AB|=![]() ,|BC|=1,
,|BC|=1,
∴|![]() |=
|=![]() =2,
=2,
∴向量(AB+BC+AC)的长度=2|![]() |=4.
|=4.
故选:A.

2、填空题:(每题3分,共36分)
7.(3分)已知平行四边形一组对角的和等于270°,那样在这个平行四边形中较小的一个内角等于__________度.
【解答】解:∵四边形ABCD是平行四边形,
∴∠B∠D,∠A=∠C,AD∥BC,
∵∠A+∠C=270°,
∴∠A=∠C=135°,
∴∠B=180°﹣∠A=45°,
∴在这个平行四边形中较小的一个内角等于45°.
故答案为:45.

8.(3分)梯形的下底长为12cm,中位线长为8cm,则它的上底长为__________cm.
【解答】解:设梯形的上底长为xcm,
由梯形中位线定理得,![]() ×(x+12)=8,
×(x+12)=8,
解得,x=4,
故答案为:4.
9.(3分)向量:![]() ﹣
﹣![]() +
+![]() =__________
=__________![]() __________.
__________.
【解答】解:由时间最法则可知:![]() ﹣
﹣![]() +
+![]() =
=![]() +(
+(![]() +
+![]() )=
)=![]() +
+![]() =
=![]() ,
,
故答案为![]()
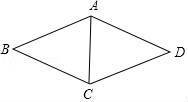
10.(3分)有一个内角等于120°的菱形,周长为12,则较短的对角线长为__________.
【解答】解:如图,在菱形ABCD中,∠BAD=120°,
则∠B+∠BAD=180°,
∴∠B=60°,
∵AB=BC=CD=DA=![]() =3,
=3,
∴△ABC为等边三角形,
∴AC=AB=3,
故答案为:3.
 [来源:学。科。网]
[来源:学。科。网]
11.(3分)如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为__________.
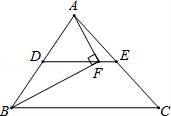
【解答】解:∵DE为△ABC的中位线,
∴DE=![]() BC=
BC=![]() ×10=5,
×10=5,
∵∠AFB为直角,D是AB的中点,即FD是直角△ABF的中线,
∴FD=![]() AB=
AB=![]() ×8=4.
×8=4.
∴EF=DE﹣FD=5﹣4=1.
故答案是:
1.
12.(3分)正方形的对角线长是![]() cm,则正方形的周长是__________,面积是______________________________.
cm,则正方形的周长是__________,面积是______________________________.
【解答】解:正方形的对角线BD长为3![]() ,
,
∵BD=![]() =3
=3![]() ,且AB=AD,
,且AB=AD,
∴AB=AD=3,
故边长为3cm,周长为12cm,面积为9cm2.
故答案为:
12cm,9cm2.
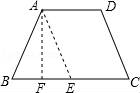
13.(3分)假如等腰梯形的腰长是5,上、下底的长分别为3、9,那样它的面积为__________.
【解答】解:如图,过点A作AE∥CD交BC于E,作AF⊥BC于F,
∵AD∥BC,
∴四边形AECD是平行四边形,
∴AD![]() =CE,AE=CD,
=CE,AE=CD,
∴AB=AE,BE=BC﹣AD=9﹣3=6,
∴BF=![]() BE=
BE=![]() ×6=3,[来源:学.科.网]
×6=3,[来源:学.科.网]
在Rt△ABF中,AF=![]() =
=![]() =4,
=4,
∴等腰梯形的面积=![]() (3+9)×4=24
(3+9)×4=24
故答案为:24.
14.(3分)如图,在矩形ABCD中,假如AB=![]() BC,BE=BC,那样∠DCE=__________度.
BC,BE=BC,那样∠DCE=__________度.

【解答】解:∵四边形ABCD是矩形,
∴∠A=∠ABC=∠DCB=90°,AD∥BC,
∵BC=BE=2AB,
∴sin∠AEB=![]() ,
,
∴∠AEB=30°,
∴∠EBC=∠AEB=30°,
∵BE=BC,
∴∠BEC=∠BCE=75°,
∴∠ECD=90°﹣75°=15°,
故答案为15.

15.(3分)假如一个平行四边形一个内角的平分线分它的一边为1:2的两部分,那样称如此的平行四边形为“协调平行四边形”,称该边为“协调边”.当“协调边”为3时,它的周长为__________.
【解答】解:如图所示:①当AE=1,DE=2时,
∵四边形ABCD是平行四边形,
∴BC=AD=3,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=1,
∴平行四边形ABCD的周长=2(AB+AD)=8;
②当AE=2,DE=1时,
同理得:AB=AE=2,
∴平行四边形ABCD的周长=2(AB+AD)=10;
故答案为:8或10.[来源:学|科|网]

16.(3分)如图,菱形ABCD中,点E是AB的中点.已知AC=8cm,BD=6cm,则OE=__________![]() __________.
__________.
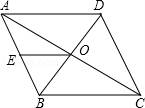
【解答】解:∵ABCD是菱形,
∴OA=OC,OB=OD,OB⊥OC,
又∵AC=8cm,BD=6cm,
∴OA=OC=4cm,OB=OD=3cm,
在直角△BOC中,
由勾股定理,得BC=![]() =5cm,
=5cm,
∵点E是AB的中点,
∴OE是△ABC的中位线,
∴OE=![]() cm.
cm.
故答案为![]() cm.
cm.
17.(3分)已知正方形ABCD的边长为6,点E是边BC的中点.联接AC、DE相交于点F,M、N分别是AC、DE的中点,则MN的长是__________.
【解答】解:连接BD,
∵E是边BC的中点,
∴BE=![]() BC=3,
BC=3,
∵四边形ABCD是正方形,
∴M是BD的中点,又N是DE的中点,
∴MN=![]() BE=1.5,
BE=1.5,
故答案为:
1.5.

18.(3分)如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是__________![]() __________.
__________.
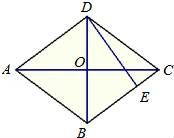
【解答】解:如图,设CD与AB1交于点O,
∵在![]() 边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=![]() ,
,
由折叠易得△ABB1为等腰直角三角形,
∴S△ABB1=![]() BA•AB1=2,S△ABE=1,
BA•AB1=2,S△ABE=1,
∴CB1=2BE﹣BC=2![]() ﹣2,
﹣2,
∵AB∥CD,
∴∠OCB1=∠B=45°,
又由折叠的性质知,∠B1=∠B=45°,
∴CO=OB1=2﹣![]() .
.
∴S△COB1=![]() O
O![]() C•OB1=3﹣2
C•OB1=3﹣2![]() ,
,
∴重叠部分的面积为:2﹣1﹣(3﹣2![]() )=2
)=2![]() ﹣2.
﹣2.
3、解答卷:(共46分)
19.(8分)如图已知:矩形ABCD,对角线AC、BD相交于点O.[来源:学.科.网]
(1)借助图中的向量表示:![]() +
+![]() =__________
=__________![]() __________;
__________;
(2)借助图中的向量表示:![]() ﹣
﹣![]() =__________
=__________![]() __________;
__________;
(3)假如|![]() |=5,|
|=5,|![]() |=5,则|
|=5,则|![]() |=__________
|=__________![]() __________.
__________.

【解答】解:(1)借助图中的向量表示:![]() +
+![]() =
=![]() ;
;
故答案为
(2)借助图中的向量表示:![]() ﹣
﹣![]() =
=![]() ;
;
故答案为![]()
(3)假如|![]() |
|![]() =5,|
=5,|![]() |=5,则|
|=5,则|![]() |=|
|=|![]() |=5
|=5![]() ,
,
∴|![]() |=
|=![]() |
|![]() |=
|=![]() ,
,
故答案为![]()
20.(10分)如图,菱形ABCD的对角线AC与BD相交于点O,已知AB=13cm,AC=24cm.
(1)求:菱形ABCD的面积;
(2)如过点D作DE⊥BC,垂足为E,求DE的长.

【解答】解:(1)∵四边形ABCD是菱形,
∴AO=OC,BO=DO,AC⊥BD
∵AC=24,AO=![]() AC=12,
AC=12,
在Rt△AOB中,AO2+BO2=AB2,
又AB=13,
∴BO=![]() =5,
=5,
∴BD=10,
∴S菱形ABCD=![]() ×10×24=120,
×10×24=120,
∴菱形ABCD的面积为120cm2.
(2)∵![]() DB×AC=BC×DE,
DB×AC=BC×DE,
∴DE=![]() ,
,
∴DE的长为![]() cm.
cm.
21.(6分)如图,点O是平行四边形ABCD的对角线AC与BD的交点,四边形OCDE是平行四边形.
求证:OE与AD互相平分.

【解答】证明:连接AE,如图.
∵四边形OCDE是平行四边形,
∴DE∥OC,DE=OC
∵O是平行四边形ABCD的对角线AC与BD的交点,
∴AO=OC.
∴DE∥OA,DE=OA
∴四边形ODEA是平行四边形,
∴OE与AD互相平分.

22.(10分)如图,梯形ABCD中,AD∥BC,B![]() C=3AD,M、N为底边BC的三等分点,连接AM,DN.
C=3AD,M、N为底边BC的三等分点,连接AM,DN.
(1)求证:四边形AMND是平行四边形;
(2)连接BD、AC,AM与对角线BD交于点G,DN与对角线AC交于点H,且AC⊥BD.试判断四边形AGHD的形状,并证明你的结论.
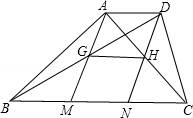
【解答】(1)证明:∵BC=3AD,BC=3MN,
∴AD=MN,
∵AD∥BC,
∴四边形AMND是平行四边形.
(2)解:四边![]() 形AGHD是菱形.
形AGHD是菱形.
∵AD∥BC,
∴∠ADG=∠MBG,
∵∠BGM=∠DGA,AD=BM,
∴△BGM≌△DGA(AAS),
∴AG=GM.
同理可得AH=HC,
∴GH是△AMC的中位线,
∴GH∥BC,![]() ,
,
∴GH∥AD,GH=AD,
∴四边形AGHD是平行四边形,
∵AC⊥BD,
∴四边形AGHD是菱形.
23.(12分)在梯形ABCD中,∠ABC=90°,AD∥BC,BC>AD,AB=8cm,BC=18cm,CD=10cm,点P从点B开始沿BC边向终点C以每秒3cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度![]() 移动,设运动时间为t秒.
移动,设运动时间为t秒.
(1)求四边形ABPQ为矩形时t的值;
(2)若题设中的“BC=18cm”改变为“BC=kcm”,其它条件都不变,要使四边形PCDQ是等腰梯形,求t与k的函数关系式,并写出k的取值范围;
(3)在移动的过程中,是不是存在t使P、Q两点的距离为10cm?若存在求t的值,若没有请说明理由.

【解答】解:(1)过点D作DH⊥BC,垂足为点H,
由题意可知:AB=DH=8,AD=BH,DC=10,
∴HC=![]() ,
,
∴AD=BH=BC﹣CH,
∵BC=18,
∴AD=BH=12,
若四边形ABPQ是矩形,则AQ=BP,
∵AQ=12﹣2t,BP=3t,
∴12﹣2t=3t
∴![]() (秒),
(秒),
答:四边形ABPQ为矩形时t的值是![]() .
.
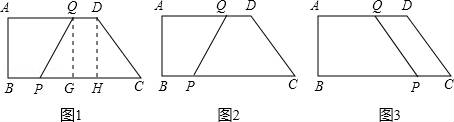
(2)由(1)得CH=6,
如图1,再过点Q作QG⊥BC,垂足为点G,
同理:PG=6,
易知:QD=GH=2t,
又BP+PG+GH+HC=BC,
∴3t+6+2t+6=k,
∴![]() ,
,
∴k的取值范围为:k>12cm,
答t与k的函数关系式是t=![]() ,k的取值范围是k>12cm.
,k的取值范围是k>12cm.
(3)假设存在时间t使PQ=10,有两种状况:
①如图2:由(2)可知:3t+6+2t+6=18,
∴![]() ,
,
②如图3:四边形PCD![]() Q是平行四边形,
Q是平行四边形,
∴QD=PC=2t,
又BP=3t,BP+PC=BC,
∴3t+2t=18,
∴![]() (秒),
(秒),
综上所述,存在时间t且![]() 秒或
秒或![]() 秒时P、Q两点之间的距离为10cm,
秒时P、Q两点之间的距离为10cm,
答:在移动的过程中,存在t使P、Q两点的距离为10cm,t的值是![]() 秒或
秒或![]() 秒.
秒.







