初三数学训练（十五）
（二次函数三）
填空题：
1、二次函数
的图象向__________平移__________个单位后，与轴仅有一个交点；
2、若
关于的函数
的图象与坐标轴有两个交点，则可取的值为__________；
3、已知抛物线
经过点
，则
的值是__________；
4、吉林某大学的校门是一抛物线形水泥建筑物，大门的地面
宽度为8米，两侧距地面4米高处各有一个挂校名横匾用的
铁环，两铁环的水平距离为6米，则校门的高为__________米；
（水泥建筑物厚度忽视不计）
5、已知抛物线
经过点
，则该抛物线的顶点坐标为__________；
6、已知抛物线 
的图象一部分如图所示，
抛物线的顶点在第一象限，且经过点
和
，则
的取值范围是__________，若，则该抛物线
的分析式是__________；
7、已知抛物线
与轴交于两点，假如有一个交点的横坐标大于2，另一个交点的横坐标小于2，并且抛物线与轴的交点在点（0，）的下方，那样
的取值范围是___________________；
8、若抛物线
的顶点在抛物线
上，则
=______________；
9、抛物线
与轴交于和两点，若
要使此抛物线经过原点应将它向右平移__________个单位；
2、解答卷：
12、如图，一位运动员在距篮下
米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为
时，达到最大高度
米，然后准确落入篮圈，已知篮圈中心到地面的距离为米，
（1）打造如图所示的直角坐标系，求抛物线的分析式；
（2）该运动员身高
米，在这次跳投中，球在头顶上方
米处出手，问：球出手时，他跳离地面的高度是多少？
10、已知二次函数，
（1）求证：无论
取何实数，此二次函数的图象与
轴都有两个交点；
（2）若此二次函数图象的对称轴为，求它的分析式；
（3）若（2）中的二次函数的图象与轴交于，与轴交于点
，是第四象限函数图象上的点，且
于，求点的坐标；
11、设抛物线
与x轴交于两个不一样的点
、
，与轴交于点.且
．
、求的值和抛物线的分析式；
、已知点在抛物线上，过点
的直线交抛物线于另一点．若点在轴上，以点、、为顶点的三角形与
相似，求点的坐标．
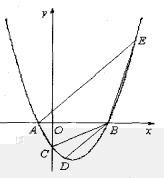
15、如图，二次函数的图象与轴交于两点,与轴相交于点,连结
,
两点的坐标分别为
，且当和
时，二次函数的函数值相等，
（１）求实数的值；
（２）若点
同时从点出发，均以每秒
个单位长度的速度分别沿
边运动，其中一个点到达终点时，另一点也随之停止运动，当运动时间为秒时，连结
，将沿翻折，点恰好落在
边上的处，求的值及点的坐标；
（３）在（２）的条件下，二次函数图象的对称轴上是不是存在点，使得以为顶点的三角形与相似？假如存在，请求出点的坐标，假如没有，请说明理由。
