§26.3二次函数的图像(1)
1、二次函数![]() 图像的对称轴是……………………………………( ).
图像的对称轴是……………………………………( ).
(A)直线x=0 (B)直线x=2 (C)直线x=4 (D)直线x= −4
2、二次函数 y=2(x-3)2+5的图象的开口方向、对称轴和顶点坐标分别为( )
A.开口向下,对称轴直线x=3,顶点坐标为(3,5)
B.开口向上,对称轴直线x=3,顶点坐标为(3,5)
C.开口向上,对称轴直线x=-3,顶点坐标为
D.开口向上,对称轴直线x=-3,顶点坐标为求m的值;
求这个二次函数的分析式,并指出开口方向、对称轴和顶点坐标.
8、已知二次函数![]() 的图像和顶点坐标为(3,2),这个图像经过平移能与
的图像和顶点坐标为(3,2),这个图像经过平移能与![]() 的图像重合,求这个二次函数的分析式.
的图像重合,求这个二次函数的分析式.
§26.3二次函数的图像(2)
1、在同一直角坐标系中,二次函数![]() 、
、![]() 、
、![]() 的图像的一同点是-
的图像的一同点是-
关于y轴对称,开口向上
关于y轴对称,当x<0时,y随x 的增大而减小
关于y轴对称,最高点是原点
关于y轴对称,顶点坐标是(0,0)
2、二次函数![]() 的图象的最高点为
的图象的最高点为![]() ,则b与c分别是 ( )
,则b与c分别是 ( )
A. b=2,c=4 B. b=2,c= -4 C. b= -2,c=4 D. b= -2,c= -4
3、如图,抛物线顶点坐标是P(1,3),函数y随自变量x的增大而减小的x的取值范围是 ( )
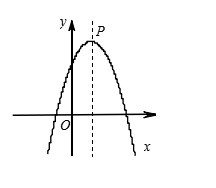 A.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
4、顶点是![]() ,且经过原点的二次函数分析式为_______________.
,且经过原点的二次函数分析式为_______________.
5、已知关于x的二次函数![]() ,当k_____________时,它的开口向上.
,当k_____________时,它的开口向上.
6、已知抛物线的顶点为(1,-3),且与y轴交于点(0,1)这个二次函数分析式为__________.
7、已知抛物线![]() ,将这条抛物线平移,得到新的抛物线的顶点坐标为(-3,5),求所得新抛物线的表达式.
,将这条抛物线平移,得到新的抛物线的顶点坐标为(-3,5),求所得新抛物线的表达式.
§26.3二次函数的图像(3)
1、二次函数![]() 的顶点和对称轴分别是 ()
的顶点和对称轴分别是 ()
A. ![]() ,直线x=1 B.
,直线x=1 B. ![]() ,直线x=4
,直线x=4
C. ![]() ,直线
,直线![]() D.
D. ![]() ,直线
,直线![]()
2、假如抛物线![]() 的顶点关于原点对称点的坐标是
的顶点关于原点对称点的坐标是![]() ,
,
那样m的值是( )
(A)5 (B)-3 -9 -1
3、抛物线y=x2-6x+3的顶点坐标是__________.
4、二次函数![]() 的顶点在y轴上,则m=______________.
的顶点在y轴上,则m=______________.
5、抛物线y=x2+2x+3关于y轴对称的分析式y=___________.
6、已知抛物线![]() 经过坐标原点O,则这条抛物线的分析式为_______________________.
经过坐标原点O,则这条抛物线的分析式为_______________________.
7、已知二次函数y=x2-4mx+1的图象的对称轴是x=2,求此二次函数分析式。
8、求抛物线![]() 与坐标轴的交点为顶点的三角形的面积。
与坐标轴的交点为顶点的三角形的面积。
9、已知二次函数的图像过抛物线![]() 的顶点和坐标原点.
的顶点和坐标原点.
求二次函数的分析式
判断点A(-2,5)是不是在这个二次函数的图像上 .
26.3二次函数的图像(4)
1、已知抛物线![]() 的顶点坐标为(3,-1),则b=_____,c=______.
的顶点坐标为(3,-1),则b=_____,c=______.
2、已知抛物线![]() 的对称轴为x=1,则m=______.
的对称轴为x=1,则m=______.
3、抛物线![]() 的开口______,对称轴是_____________,顶点是_______.
的开口______,对称轴是_____________,顶点是_______.
4、用配办法将下列函数分析式改写成![]() 的形式,并指出开口方向、顶点坐标和对称轴。
的形式,并指出开口方向、顶点坐标和对称轴。
⑴![]() ⑵
⑵![]()
⑶ ![]() ⑷
⑷![]()
5、指出下列函数的开口方向、对称轴、顶点坐标和变化状况
(1)![]()
(2)![]()
6、已知:二次函数![]() ,当x<-2时y随x的增大而减小;当x>-2时,y随x的增大而增大,求当x=1时,y值.
,当x<-2时y随x的增大而减小;当x>-2时,y随x的增大而增大,求当x=1时,y值.
§26.3二次函数的图像(5)
1、二次函数![]() 的对称轴是 ( )
的对称轴是 ( )
A.直线x=-2 B. 直线x=-4
C. 直线x=1 D. 直线x=-1
2、已知函数![]() 的图像经过点(0,3),c的值是 ( )
的图像经过点(0,3),c的值是 ( )
A.0 B.1 C.2 D.3
3、二次函数![]() 的开口___________,对称轴是____________.
的开口___________,对称轴是____________.
4、二次函数![]() 图像的顶点坐标是__________________.
图像的顶点坐标是__________________.
5、二次函数![]() 的开口___________,对称轴是______________,顶点是_________________.
的开口___________,对称轴是______________,顶点是_________________.
6、指出下列二次函数图像的开口方向、对称轴和顶点坐标.
(1)![]()
(2)![]()
7、已知二次函数图像经过下列点,求二次函数的分析式:
(1)(0,-1),(1,-1),(2,3)
(2)(0,0),(2,0),(-3,3)
§26.3二次函数的图像(6)
1、抛物线![]() 的顶点坐标是 ( )
的顶点坐标是 ( )
A. B.
C. D.
2、抛物线![]() 经过点(2,-12),则c=_____________.
经过点(2,-12),则c=_____________.
3、若二次函数![]() 与y轴的交点坐落于(0,2)的下方了,则k的取值范围是____________________.
与y轴的交点坐落于(0,2)的下方了,则k的取值范围是____________________.
4、抛物线![]() 的顶点在x轴上,则m=________________.
的顶点在x轴上,则m=________________.
5、已知:等边△ABC的边长是4,A点坐标为(-1,0),B点在x轴正半轴上,C点在第一象限,AC与y 轴交于D点.
(1)求B、C、D三点的坐标;
(2)求经过A、B、D三点的抛物线分析式
6、某商场以每件40元的价格购进一种产品,试销中发现,这种产品天天的销量m(件)与每件的销价格x
分析:平移后分析式是![]()
4.答案:![]()
分析:![]() 绕着顶点旋转
绕着顶点旋转![]() 后顶点不变,开口方向相反
后顶点不变,开口方向相反
__________
5.答案:右;2;上;3
分析:左加右减,上加下减,注意先后
6.答案:二次函数分析式为![]()
分析:设![]() ,代入(1,2)
,代入(1,2)
![]() ,
,![]()
∴二次函数分析式为![]()
7.答案: m的值是-3 二次函数的分析式为![]() ,开口方向向下,对称轴是直线
,开口方向向下,对称轴是直线![]() ,顶点坐标是(-2,-5)
,顶点坐标是(-2,-5)
分析: ![]() ,
,![]()
当![]() 时,
时,![]() ,舍,
,舍,
∴![]()
二次函数的分析式为![]() ,开口方向向下,对称轴是直线
,开口方向向下,对称轴是直线![]() ,顶点坐标是(-2,-5)
,顶点坐标是(-2,-5)
8.答案:二次函数的分析式是![]()
分析:∵这个图像经过平移能与![]() 的图像重合
的图像重合
∴![]() ,
,
∵ 顶点坐标为(3,2)
∴这个二次函数的分析式是![]()
§26.3二次函数的图像(2)
1.答案:D
分析:开口方向不同,则增减性,最高点最低点也不同
2.答案:D
分析:![]()
3.答案:C
分析:对称轴是直线![]()
4.答案:![]()
分析:设![]() ,代入(0,0)
,代入(0,0)
![]() ,
,![]()
5.答案:![]()
分析:![]() ,
,![]()
6.答案:![]()
分析:设![]() ,代入(0,1)
,代入(0,1)
![]() ,
,![]()
二次函数分析式为![]()
7.答案:新抛物线的表达式为![]()
分析:∵平移前抛物线![]()
∴a=-2
∵新的抛物线的顶点坐标为(-3,5)
∴新抛物线的表达式为![]()
§26.3二次函数的图像(3)
1.答案:C
分析:![]()
2.答案:A
分析:顶点坐标(1,3),分析式为![]()
3.答案:(3,-6)
分析:![]()
4.答案:-2
分析: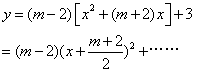
∵顶点在y轴上
∴![]() ,
,![]()
5.答案:![]()
分析:![]() 关于y轴对称的分析式
关于y轴对称的分析式![]()
6.答案:![]()
分析:代入(0,0),![]() ,
,![]()
7.答案:二次函数分析式为![]() 或
或![]()
分析:y=x2-4mx+1= ![]()
![]()
∵图象的对称轴是x=2
∴![]() ,
,![]() ,
,![]() ,
,![]() 或2
或2
∴此二次函数分析式为![]() 或
或![]()
8.答案:三角形的面积为10
分析:![]() =
=![]()
与x轴的交点为(-1,0)和(4,0),与y轴的交点为(0,-4)
三角形的面积为![]()
9.答案: 二次函数的分析式为![]()
点A(-2,5)不在这个二次函数的图像上
分析:![]() ,顶点坐标为(-1,2)
,顶点坐标为(-1,2)
设![]() ,代入(0,0)
,代入(0,0)
![]() ,
,![]()
二次函数的分析式为![]()
当x=-2时,y=0,点A(-2,5)不在这个二次函数的图像上
26.3二次函数的图像(4)
1.答案:-12,17
分析:![]()
2.答案:-2
分析:![]()
3.答案:向下;直线x=![]() ;
;![]()
分析:![]() =
=![]()
4.答案:![]() ;开口向上;
;开口向上;
顶点![]() ;对称轴直线x= -2
;对称轴直线x= -2
分析:![]()
![]()
![]()
答案:![]() ;开口向下;
;开口向下;
顶点![]() ;对称轴直线x=
;对称轴直线x=![]()
分析:![]()
![]()
![]()
答案:![]() ;开口向上; 答案:
;开口向上; 答案:![]() ;开口向下;
;开口向下;
顶点![]() ;对称轴直线x=
;对称轴直线x=![]() 顶点
顶点![]() ;对称轴直线x= 2
;对称轴直线x= 2
分析:![]() 分析:
分析:![]()
![]()
![]()
![]()
![]()
5.答案:开口向上;对称轴直线x=2,顶点坐标(2,-6);
对称轴左边部分降低,右边部分上升
分析:![]()
答案:开口向下;对称轴直线x= -2,顶点坐标(-2,- ![]() );
);
对称轴左边部分上升,右边部分降低
分析:![]()
6.答案:y值为25
分析:对称轴是直线x= -2,
![]()
∴m=-16;分析式是![]()
当x=1时,y=4+16+5=25
§26.3二次函数的图像(5)
1.答案:C
分析:图像与x轴的交点是(-2,0)(4,0),对称轴是直线x=1
2.答案:D
分析:二次函数的图像与y轴交于(0,c)
3.答案:向上;直线x=-1
分析:图像与x轴的交点是(-5,0)(3,0),对称轴是直线x=-1
4.答案:(1,9)
分析:图像与x轴的交点是(-2,0)(4,0),对称轴是直线x=1,当x=1时,y=9
5.答案:向上;直线x=-1;(-1,-1)
分析:![]()
6.答案:开口向上;对称轴是直线x=-1;顶点坐标是(-1,-![]() )
)
分析:图像与x轴的交点是(2,0)(-4,0),对称轴是直线x=-1,
当x=-1时,y=-![]() ,顶点坐标是(-1,-
,顶点坐标是(-1,-![]() )
)
答案:开口向下;对称轴是直线x=-![]() ;顶点坐标是(-
;顶点坐标是(-![]() ,
,![]() )
)
分析:![]()
7.答案:二次函数的分析式为![]()
分析:设![]()
代入(1,-1),(2,3)
![]()
解得![]()
∴分析式为![]()
答案:二次函数的分析式为![]()
分析:设![]()
代入(-3,3)
![]() ,
,![]()
∴分析式为![]()
§26.3二次函数的图像(6)
1.答案:B
分析:图像与x轴的交点是(3,0)(-1,0),对称轴是直线x=1,
当x=1时,y=-8,顶点坐标是(1,-8)
2.答案:![]()
分析:代入(2,-12),![]() ,
,![]()
3.答案:![]()
分析:![]() ,
,![]()
4.答案:![]()
分析:对称轴是直线![]() ,当
,当![]() 时,y=0,
时,y=0,
∴![]() ,
,![]()
5.答案:(1)B(3,0),C(1,![]() )(2)抛物线分析式为
)(2)抛物线分析式为![]()
分析:(1)∵等边△ABC的边长是4,A点坐标为(-1,0),B点在x轴正半轴上
∴B(3,0),高为![]()
∵C点在第一象限
∴C(1,![]() )
)
(2)可求得点D(0,![]() )
)
设![]()
代入(0,![]() )
)
![]() ,
,![]()
∴抛物线分析式为![]()
答案:(1)y与每件的销价格x之间的函数分析式是![]()
(2)每件产品的价格定位60元比较合适,最大的销售收益为800元.
6.分析:(1)![]()
![]()
![]()
![]()
∴y与每件的销价格x之间的函数分析式是![]()
(2)![]()
![]()
![]()
顶点是(60,800)
答:每件产品的价格定位60元比较合适,最大的销售收益为800元。







