23.2 解直角三角形及其应用
1、选择题（共4题）
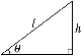
1．如图，已知一商场自动扶梯的长为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为θ，则tan θ的值等于．
A． 
B． 
C． 
D． 
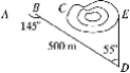
2．如图，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B，取∠ABD＝145°，BD＝500 m，∠D＝55°，要A，C，E成一直线，那样开挖点E离点D的距离是．
A．500sin 55° m B．500cosplay 55° m
C．500tan 55° m D． 
3.等腰三角形的两条边长分别是4 cm、9 cm，则等腰三角形的底角的余弦值是
A. 
B. 
C. 
D. 
4.如图，两建筑物的水平距离为a米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低建筑物CD的高度为
A.a B.atanα C.a D.a
2、填空题（共5题）
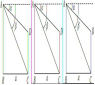
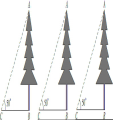
5．如图，在坡度为1∶2的山坡上种树，需要株距是6 m，则斜坡上相邻两树间的坡面距离是__________ m.
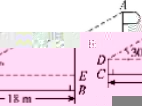
6．如图，小明在操场上距离旗杆18 m的C处，用测角仪测得旗杆AB的顶端A的仰角为30°，已知测角仪CD的高为1.4 m，那样旗杆AB的高为________ m．
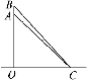
7.有人说，数学家就是不需要爬树或把树砍倒就可以了解树高的人.小敏想了解校园内一棵大树的高度（如图），他测得CB=10米，∠ACB=50°，请你帮他算出树高AB,约为________________米.
（注：①树垂直于地面；②供使用数据：sin50°≈0.77，cosplay50°≈0.64，tan50°≈1.2）
3、计算与解答卷（共4题）
8. 如图，在亚丁湾一海域实行护航任务的我海军某军舰由东向西行驶．在航行到B处时，发现灯塔A在我军舰的正北方向500米处；当该军舰从B处向正西方向行驶至C处时，发现灯塔A在我军舰的北偏东60°的方向．求该军舰行驶的路程．
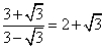
9．如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6 km，仰角是43°.1 s后，火箭到达B点，此时测得BC的距离是6.13 km，仰角为45.54°，解答下列问题：
火箭到达B点时距离发射点有多远?
火箭从A点到B点的平均速度是多少?
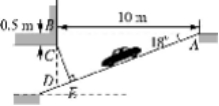
10．某商场为缓解我市“停车难”问题，拟建造地下停车库，如图是该地下停车库坡道入口的设计示意图，其中，AB⊥BD，∠BAD＝18°，C在BD上，BC＝0.5 m．依据规定，地下停车库坡道入口上方要张贴限高标志，以便告知驾驶员所开车辆能否安全驶入．小明觉得CD的长就是所限制的高度，而小亮觉得应该以CE的长作为限制的高度．小明和小亮哪个说的对？请你判断并计算出正确的结果．
11．关于三角函数有如下的公式：
sin＝sin αcosplay β＋cosplay αsin β，①
cosplay＝cosplay αcosplay β－sin αsin β，②
tan＝ 
．③
借助这类公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如
tan 105°
＝tan
＝ 
＝－．
依据上面的常识，你可以选择合适的公式解决下面的实质问题：
如图，直升飞机在一级建造师筑物CD上方A点处测得建筑物顶端D点的俯角α为60°，底端C点的俯角β为75°，此时直升飞机与建筑物CD的水平距离BC为42米，求建筑物CD的高．
参考答案
1.A
2.分析：∵∠E＝180°－55°－35°＝90°，
∴DE＝BD·cosplay D＝500cosplay 55°．
答案：B
3.分析：依据构成三角形的条件，该等腰三角形的三边长为9、9、4，∴其底角的余弦值为 .
答案：C
4.分析:过D点作AB的垂线交AB于E点，在
Rt△ADE中,∠ADE=α,DE=a,
∴AE=a·tanα.
在Rt△ABC中,∠ACB=β,BC=a,
∴AB=a·tanβ.
∴CD=AB－AE=a·tanβ－a·tanα.
答案:D
5. 
6.分析：AE＝DE·tan 30°＝18× ≈10.4，
EB＝1.4 m，
∴AB＝AE＋BE＝10.4＋1.4＝11.8．
答案：
11.8
7.分析:AB=BC·tanC=12.
答案:12
8.解：由已知，可得∠ACB=30°.
在Rt△ABC中，∠ACB=30°，AB=500.
∵tan∠ACB= 
，
∴BC= 
= 
.
因此该军舰行驶的路程为 米．
9.解：在Rt△OCB中，sin 45.54°＝ 
，OB＝6.13×sin 45.54°≈4.38，
答：火箭到达B点时距发射点约4.38 km.
在Rt△OCA中，sin 43°＝ 
，
∴OA＝6×sin 43°≈4.09，
v＝÷t＝÷1≈0.3．
答：火箭从A点到B点的平均速度约为0.3 km/s.
10.解：小亮的说法正确．
在△ABD中，∠ABD＝90°，∠BAD＝18°，BA＝10，
∴tan∠BAD＝ 
.
∴BD＝10×tan 18°.
∴CD＝BD―BC＝10×tan 18°－0.5.
在△ABD中，∠CDE＝90°－∠BAD＝72°，
∵CE⊥ED，
∴sin∠CDE＝ 
.
∴CE＝sin∠CDE×CD＝sin 72°×≈2.6．
答：CE为2.6 m，即限高为2.6 m.
11.解：过点D作DE⊥AB于E，
依题意，在Rt△ADE中，∠ADE=∠α=60°，
AE=ED·tan 60°=BC·tan 60°= 
.
在Rt△ACB中，∠ACB=∠β=75°，AB=BC·tan 75°.
∵tan 75°=tan
= 
= ，
∴AB=42×=84+ ，CD=BE=AB-AE=84+ 
=84．
答：建筑物CD的高为84米．
