曹二高中三年级上学期周测试题二
2020.10
1、填空题:
1、若复数z=1+i,则|z|=__________
2、椭圆![]() 的长轴长为__________
的长轴长为__________
3、函数![]() 的概念城是__________
的概念城是__________
4、圆锥的底面半径为1,高为3,则圆锥的侧面积为__________
5、函数f=x3的反函数是__________
6、幂函数![]() 是偶函数,且在上单调递减,则m的值为__________
是偶函数,且在上单调递减,则m的值为__________
7、若数列{an}的通项公式为an=2n-1,则![]() __________
__________
8、若关于x的不等式|x-1|+|x-2|>a的解集为R,则实数a的取值范围是__________
9、已知△ABC的面积为![]() ,AC=
,AC=![]() ,∠ABC=
,∠ABC=![]() ,则△ABC的周长等于__________
,则△ABC的周长等于__________
10、已知集合A={0,2,3,9},函数y=f的概念域为A,值域为B,且A∩B=B,那样该函数的值域的不同状况有__________种
11、已知圆x2+y2=4,过点P作两茶互相垂直的直线![]() ,其中
,其中![]() 交该圆于A,B两点,
交该圆于A,B两点,![]() 交该圆于C,D两点,则|AB|+|CD|的最大值是__________
交该圆于C,D两点,则|AB|+|CD|的最大值是__________
已知概念在R上的函数y=满足f=f,当![]() 时,f=|lgx|,若方程f=m有四个零点
时,f=|lgx|,若方程f=m有四个零点![]() ,则
,则![]() 的取值范围是__________
的取值范围是__________
2、选择题:
13、已知x∈R,则“x≥1”是“x>3”的( )
A、充分非必要条件B、必要非充分条件c、充要条件D、既非充分也非必要条
14、已知m和n是两条不一样的直线,![]() 和
和![]() 是两个不重合的平面,则下列给出的条件中能推出m⊥
是两个不重合的平面,则下列给出的条件中能推出m⊥![]() 的是
的是
A、![]() ⊥
⊥![]() 且m
且m![]()
![]() B、
B、![]() ⊥
⊥![]() 且m∥
且m∥![]() C、m∥n且n⊥
C、m∥n且n⊥![]() D、m⊥n且n∥
D、m⊥n且n∥![]()
15、已知非零向量![]() ,若点B关于直线OA的对称点为B1,则向量
,若点B关于直线OA的对称点为B1,则向量![]() 为()
为()
A、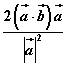 B、
B、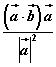 C、
C、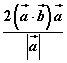 D、
D、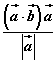
16、已知在R上的函数f满足f=-f,函数g=2,若方程f=g有2021个解,记为xi,则x1+x2+…+x2021=
A、2020 B、4040 C、2021 D、4042
3、解答卷
17、如图所示,在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=4,E、F分别是棱AB、BC的中点,点P是棱A1B1上的动点.
求异面直线EF、AC1所成角的大小;
求以E、F、A、P为顶点的三棱锥的体积.

18、已知函数f=sin2x+![]() cosplay2x-m,x∈R,且f的最大值为1.
cosplay2x-m,x∈R,且f的最大值为1.
求m的值,并求f的单调递增区间;
在△ABC中,角A、B、C的对边a、b、c,若f=![]() ,且
,且![]() a=b+c,试判断△ABC的形状.
a=b+c,试判断△ABC的形状.
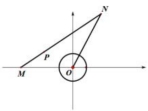
19、某旅游景点在水上设置了一个娱乐游戏设置,如图所示,O为水波圈发射器,其发射的水波圈秒时的半径为r=![]() ,MN是铺设在水面上的直线段型浮桥,浮桥的两端点M、N固定在水岸边,游戏规定:当O处刚产生水波圈时,游戏参与者从M端出发,沿浮桥跑向N端,若该参与者在浮桥上运动过程中,从点O出发的水波圈一直未能达到此人跑动时的地方,则认定游戏参与者过关;不然,认定不过关,已知MO=10米,∠MMO=45°,tan∠MON=-3,小明参与该游戏,并以
,MN是铺设在水面上的直线段型浮桥,浮桥的两端点M、N固定在水岸边,游戏规定:当O处刚产生水波圈时,游戏参与者从M端出发,沿浮桥跑向N端,若该参与者在浮桥上运动过程中,从点O出发的水波圈一直未能达到此人跑动时的地方,则认定游戏参与者过关;不然,认定不过关,已知MO=10米,∠MMO=45°,tan∠MON=-3,小明参与该游戏,并以![]() 米/秒的速度从浮桥M端跑向N端.
米/秒的速度从浮桥M端跑向N端.
求小明从浮桥M端跑至N端所需的时间;
请问小明是不是过关?请说明理由.
20、对于函数y=f,若存在区间[m,n],当x∈[m,n]时,f的值域为[km,kn],则称y=f为“k倍值函数”,[m,n]是其“k倍值区间”![]() .
.
写出函数y=x2的“2倍值区间”;
若函数f=loga是“![]() 倍值函数”求实数t的取值范围;
倍值函数”求实数t的取值范围;
若函数g=![]() 是“1倍值函数”,求t的取值范围,并求当t变化时,n-m的最大值.
是“1倍值函数”,求t的取值范围,并求当t变化时,n-m的最大值.
21、对数列{an},规定{△an}为数列{an}的一阶差分数列,其中△an=an+1-an,规定{△2an}为{an}的二阶差分数列,其中△2an =△an+1-△an.
数列{an}的通项公式an=n2,求数列{△an}与{△2an}的通项公式;
数列{bn}是公比为q的正项等比数列,且q≥2,对于任意的n∈N*,都存在m∈N*,使得△2bn=bm,求q所大概的取值构成的集合;
已知正项数列{cn}满足△2cn=0.
①求证: {cn}是等差数列;
②设{cn}的前n项和Sn,若对于满足m+n=2k,m≠n的任意正整数m、n、k,都有cm≠cn,且不等式Sm+Sn>tSk恒成立,求实数t的最大值.
参考答案:
1、填空题
1、![]() ; 2、4; 3、
; 2、4; 3、![]() ; 4、
; 4、![]() ; 5、
; 5、![]() ; 6、1;
; 6、1;
7、![]() ; 8、
; 8、![]() ; 9、
; 9、![]() ; 10、15; 11、
; 10、15; 11、![]() ; 12、
; 12、![]() ;
;
2、选择题
13-16 BCAC
3、解答卷
17、(1)![]() ;(2)2.
;(2)2.
18、(1)1,![]() ;(2)Rt三角形.
;(2)Rt三角形.
19、(1)5秒;(2)小明过关.
20、(1)![]() ;(2)t<0;(3)
;(2)t<0;(3)![]()
21、(1)△an=2n+1,△![]() ;(2)
;(2)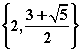 ;(3)①证明略;②2.
;(3)①证明略;②2.







