黄浦区 2017 学年第一学期期末考试试题
初二数学
(满分 100 分,考试时间 90 分钟)
1、选择题(本大题共 6 题,每题 3 分,满分 18 分)
1.![]() 的一个有理化因式可以是………………………………………………( ).
的一个有理化因式可以是………………………………………………( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.下列关于 x 的方程肯定有实数解的是……………………………………( ).
(A) x 2 − x + 2 = 0 (B) x 2 + x − m = 0
(C)![]() x 2 − 2 x + 1 = 0 (D) x 2 − mx − 1 = 0
x 2 − 2 x + 1 = 0 (D) x 2 − mx − 1 = 0
3.已知反比率函数 y = ![]() 的图像经过点( 3 ,−2 ),则 k 的值是………………………( )
的图像经过点( 3 ,−2 ),则 k 的值是………………………( )
(A)![]() ; (B) 6 ; (C) −6 ; (D) −
; (B) 6 ; (C) −6 ; (D) − ![]() .
.
4.下列定理中,没逆定理的是………………………………………( )
(A)两直线平行,同旁内角互补;(B)两个全等三角形的对应角相等;
(C)直角三角形的两个锐角互余;(D)两内角相等的三角形是等腰三角形.
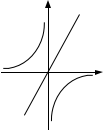
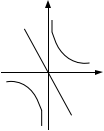
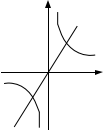
5.已知函数 y = ![]() 中,在每一个象限内, y 随 x 的增大而增大,那样它和函数
中,在每一个象限内, y 随 x 的增大而增大,那样它和函数
y = −kx 在同一直角坐标平面内的大致图像是………………………( ).

 y y y y
y y y y
O O O O
x x x x
6.如图,在 Rt△ ABC 中,∠ACB = 900 ,假如 CD 、CM 分别是斜边上的高和中线,AC = 2 ,
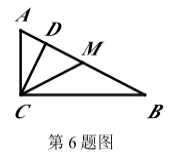 BC =4,那样下列结论中错误的是 ……………( ).
BC =4,那样下列结论中错误的是 ……………( ).
∠ACD = ∠B ; (B) CM =![]()
∠B =30° CD =![]()
2、填空题(本大题共 12 题,每题 2 分,满分 24 分)
7.化简:![]() __________
__________
8.计算![]() __________
__________
9.方程 2x2 = 3x 的解是____________________.
10.在实数范围内因式分解: x 2 − 2 x − 1 =_________________ .
11.函数y =![]() 的概念域是__________
的概念域是__________
12.已知 f =![]() , 那样 f =____________________.
, 那样 f =____________________.
13.已知关于 x 的方程 x2-2x+m-4=0 有两个不相等的实数根,那样 m 的取值范围 是____________________.
14.假如反比率函数 y =![]() 的图像在 x<0 的范围内,y 随 x 的增大而减小,那样 m 的取
的图像在 x<0 的范围内,y 随 x 的增大而减小,那样 m 的取
值范围是____________________.
15.经过已知点 A 和点 B 的圆的圆心的轨迹是____________________.
16.若△ABC 的三条边分别为 5、12、13,则△ABC 之最长边上的中线长为______________________________________________________________________.
17.如图,在△ABC 中,边 BC 的垂直平分线分别与 AC、BC 交于点 D、E,假如 AB=CD,
∠C=20°,那样∠A=______________________________度.
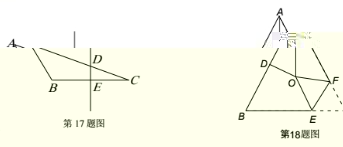 18.如图,△ABC 中,AB=AC,∠BAC=56°,∠BAC 的平分线与 AB 的垂直平分线交于点 O, 将∠C 沿 EF(E 在 BC 上,F 在 AC 上)折叠,点 C 与点 O 恰好重合,则∠OEC 为 ____________________ 度.
18.如图,△ABC 中,AB=AC,∠BAC=56°,∠BAC 的平分线与 AB 的垂直平分线交于点 O, 将∠C 沿 EF(E 在 BC 上,F 在 AC 上)折叠,点 C 与点 O 恰好重合,则∠OEC 为 ____________________ 度.
3、简答卷(本大题 4 题,第 19、20 题每题 5 分,第 21、22 题每题 6 分,满分 22 分)
19.计算![]()
20.解方程: 2 − = 12
21.如图,∠AOB= 600 ,点 C 在 OB 上.
(1)求作:∠AOB 内部一点 P,使点 P 到∠AOB 的两边 OA、OB 的距离相 等,且 PO=PC;
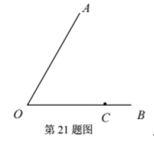 (不需要写出作法和证明,但需要保留作图痕迹,并写出结论)
(不需要写出作法和证明,但需要保留作图痕迹,并写出结论)
(2)若上题中的点 P 到 OA 的距离是 4cm,则 PC 的长是____________________cm
22.已知:点 P(m,4)在反比率函数 y = −![]() 的图像上,正比率函数的图像经过点 P 和点
的图像上,正比率函数的图像经过点 P 和点
Q(6,n).
(1)求正比率函数的分析式;
(2)求 P、Q 两点之间的距离.
4、解答卷(本大题 4 题,第 23、24 题每题 6 分,第 25、26 题每题 7 分,满分 26 分)
23.小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离 s
与骑车的时间 t(分钟)之间的函数关系如图所示,请依据图中信息回答下列问题:
(1)小强去学校时下坡路长______________________________千米;
(2)小强下坡的速度为____________________千米/分钟;
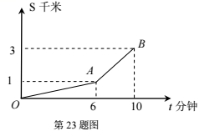 (3)若小强回家时按原路返回,且上坡的速度不变,下坡的 速度也不变,那样回家骑车走这段路的时间是__________分 钟.
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的 速度也不变,那样回家骑车走这段路的时间是__________分 钟.
24.已知:如图,在△ABC 中, ∠ACB = 45° ,AD 是边 BC 上的高, G 是 AD 上
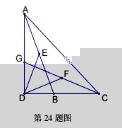 一点,联结 CG ,点 E 、 F 分别是 AB 、 CG 的中点,且 DE = DF .
一点,联结 CG ,点 E 、 F 分别是 AB 、 CG 的中点,且 DE = DF .
求证:BD=GD.
 25.如图,点 P 的坐标为(2,
25.如图,点 P 的坐标为(2,![]() ),过点 P 作 x 轴的平行线交 y 轴于点 A,交双曲线 y =
),过点 P 作 x 轴的平行线交 y 轴于点 A,交双曲线 y =![]()
于点 N;作 PM⊥AN 交双曲线 y =![]() 于点 M,联结 AM,且 PN=4.
于点 M,联结 AM,且 PN=4.
(1)求 k 的值.
(2)求△APM 的面积
26.到三角形三条边距离相等的点,叫做此三角形的内心,由此大家引入
如下概念:到三角形的两条边距离相等的点,叫做此三角形的准内心.
举例:如图(1)若 AD 平分∠CAB,则 AD 上的点 E 为△ABC 的准内心
应用:(1)如图(2)AD 为等边三角形 ABC 的高,准内心 P 在高 AD 上
且 PD= ![]() AB ,则∠BPC 的度数为____________________度.
AB ,则∠BPC 的度数为____________________度.
(2)如图(3)已知直角△ABC 中斜边 AB=5,BC=3,准内心 P 在 BC 边上,
 求 CP 的长.
求 CP 的长.
5、综合题(本大题第(1)小题 3 分,第(2)小题 3 分,第(3)小题 4 分,满分 10 分)
27.在 Rt△ ABC 中, ∠C = 90° , ∠B = 30° , AB = 10 ,点 D 是射线 CB 上的一个动点,
△ADE 是等边三角形,点 F 是 AB 的中点,联结 EF .
(1)如图(1),当点 D 在线段 CB 上时,
①求证:△ AEF ≌△ ADC ;
②联结 BE,设线段 CD = x ,线段 BE = y ,求 y 关于 x 的函数分析式及概念域;
 (2)当 ∠DAB = 150 时,求△ADE 的面积.
(2)当 ∠DAB = 150 时,求△ADE 的面积.







