2020年上海中考数学各区域模拟考试分类（上海专版）（一）——方程与不等式
一．选择题
1．（2020•浦东新区三模）假如a＜b，那样下列结论不正确的是（）
A．a+3＜b+3 B．a﹣3＜b﹣3 C．3a＜3b D．﹣3a＜﹣3b
2．（2020•路桥区模拟）某公司拟购进A，B两种型号机器人．已知用240万元购买A型机器人和用360万元购买B型机器人的台数相同，且B型机器人的单价比A型机器人多10万元．设A型机器人每台x万元，则所列方程正确的是（）
A．
B．
C．
＝10 D．
＝10
3．（2020•虹口区二模）假如关于x的方程x2﹣4x+m＝0有两个不相等的实数根，那样m的取值范围为（）
A．m≤4 B．m＜4 C．m≥4 D．m＞4
4．（2020•奉贤区二模）假如关于x的一元二次方程x2﹣2x+m＝0有两个不相等的实数根，那样实数m的值可以是（）
A．0 B．1 C．2 D．3
5．（2020•静安区二模）假如关于x的方程x2+2x+m＝0有实数根，那样m的取值范围是（）
A．m＜1 B．m≤1 C．m＞1 D．m≥1
6．（2020•黄浦区二模）下列方程没实数根的是（）
A．x2＝0 B．x2+x＝0 C．x2+x+1＝0 D．x2+x﹣1＝0
7．（2020•松江区二模）不等式组
的解集是（）
A．x＞﹣2 B．x＜﹣2 C．x＞2 D．x＜2
8．（2020•徐汇区二模）下列方程中，有实数根的是（）
A．x2+1＝0 B．x2﹣1＝0 C．
＝﹣1 D．
＝0
9．（2020•崇明区二模）假如a＞b，那样下列结论中肯定成立的是（）
A．2﹣a＞2﹣b B．2+a＞2+b C．ab＞b2 D．a2＞b2
10．（2020•闵行区二模）方程x2﹣2
x+3＝0根的状况（）
A．有两个不相等的实数根 B．有一个实数根
C．无实数根 D．有两个相等的实数根
二．填空题
11．（2020•无锡二模）方程x2+x﹣2＝0的解是__________．
12．（2020•普陀区二模）假如把二次方程x2﹣xy﹣2y2＝0化成两个一次方程，那样所得的两个一次方程分别是__________．
13．（2020•普陀区二模）假如关于x的方程（x﹣2）2＝m﹣1没实数根，那样m的取值范围是__________．
14．（2020•普陀区二模）方程
＝﹣x的解是__________．
15．（2020•中宁县一模）某品牌的衬衫每件进价是80元，价格为120元，“五•一”期间搞活动打9折，则销售1件衬衫的价值是__________元
16．（2020•黄浦区二模）假如一个矩形的一边长是某个正方形边长的2倍，另一边长比该正方形边长少1厘米，且矩形的面积比该正方形的面积大8平方厘米，那样该正方形的边长是__________厘米．
17．（2020•杨浦区二模）不等式组
的解集是__________．
18．（2020•松江区二模）方程组
的解是__________．
19．（2020•嘉定区二模）方程
＝3的根是__________．
20．（2020•静安区二模）方程
＝0的根为__________．
三．解答卷
21．（2020•普陀区二模）解不等式组：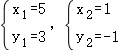
，并把解集在数轴上表示出来．
22．（2020•长宁区二模）解方程：﹣
＝
．
23．（2020•金山区二模）解方程组：．
24．（2020•黄浦区二模）解方程组：．
25．（2020•松江区二模）解方程：
﹣
＝2．
26．（2020•静安区二模）解方程：
＝1．
27．（2020•虹口区二模）解不等式组：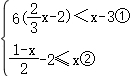
并把解集在数轴上表示出来．
28．（2020•浦东新区二模）学校拓展“书香校园”活动，购买了一批图书．已知购买科普类图书花费了10000元，购买文学类图书花费了9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普类图书的数目比购买文学类图书数目少100本，科普类图书平均每本的价格是多少元？
参考答案
一．选择题
1．解：A、两边都加3，不等号的方向不变，故A结论正确；
B、两边都减3，不等号的方向不变，故B结论正确；
C、两边都乘以3，不等号的方向不变，故C结论正确；
D、两边都乘以﹣3，不等号的方向改变，故D结论不正确．
故选：D．
2．解：设A型机器人每台x万元，则B型机器人每台（x+10）万元，
依题意，得：
＝
．
故选：A．
3．解：依据题意知△＝（﹣4）2﹣4m＞0，
解得m＜4，
故选：B．
4．解：依据题意得△＝（﹣2）2﹣4m＞0，
解得m＜1，
所以m可以取0．
故选：A．
5．解：依据题意知△＝22﹣4m≥0，
解得m≤1，
故选：B．
6．解：A．此方程辨别式△＝02﹣4×1×0＝0，故方程有两个相等的实数根；
B．此方程辨别式△＝12﹣4×1×0＝1＞0，故方程有两个不相等的实数根；
C．此方程辨别式△＝12﹣4×1×1＝﹣3＜0，故方程没实数根；
D．此方程辨别式△＝12﹣4×1×（﹣1）＝5＞0，故方程有两个不相等的实数根；
故选：C．
7．解：解不等式x+2＞0，得：x＞﹣2，
解不等式6﹣2x＜2，得：x＞2，
则不等式组的解集为x＞2，
故选：C．
8．解：A、方程变形得x2＝﹣1＜0，故没实数根，此选项错误；
B、方程变形得x2＝1，故有实数根，此选项正确；
C、二次根式非负，故没实数根，此选项错误；
D、方程两边乘x﹣1得1＝0，没实数根，此选项错误．
故选：B．
9．解：A、∵a＞b，
∴2﹣a＜2﹣b，故本选项错误，不符合题意；
B、∵a＞b，
∴2+a＞2+b，故本选项正确，符合题意；
C、∵a＞b，
∴当b＞0时，ab＞b2，当b＜0时，ab＜b2，不可以判断ab和b2的大小，故本选项错误，不符合题意；
D、∵a＞b，
不可以判断a2和b2的大小，故本选项错误，不符合题意；
故选：B．
10．解：由题意可知：△＝（﹣2）2﹣4×1×3＝12﹣12＝0，
故选：D．
二．填空题（共10小题）
11．解：（x+2）（x﹣1）＝0，
x+2＝0或x﹣
1＝0，
所以x1＝﹣2，x2＝1．
故答案为x1＝﹣2，x2＝1．
12．解：∵x2﹣xy﹣2y2＝0，
∴（x﹣2y）（x+y）＝0，
∴x﹣2y＝0或x+y＝0．
故答案为：x﹣2y＝0或x+y＝0
13．解：∵关于x的方程（x﹣2）2＝m﹣1没实数根，
∴m﹣1＜0，
解得m＜1，
所以m的取值范围是m＜1．
故答案为：m＜1．
14．解：把方程
＝﹣x两边平方，得
5x＝x2，
∴x2﹣5x＝0，
∴x（x﹣5）＝0，
∴x＝0或x﹣5＝0，
∴x1＝0，x2＝5．
检验：把x1＝0，x2＝5代入方程＝﹣x，
可知x1＝0是原方程的根，x2＝5是原方程的增根，
所以原方程的解为x＝0．
故答案为：x＝0．
15．解：设销售1件衬衫的价值为x元，
依题意，得：80+x＝120×0.9，
解得：x＝28．
故答案为：28．
16．解：设正方形的边长为x厘米，则矩形的一边长为2x厘米，另一边长为（x﹣1）厘米，
由题意得，2x（x﹣1）﹣x2＝8，
整理得，x2﹣2x﹣8＝0，
解得，x1＝﹣2（舍去），x2＝4，
故答案为：4．
17．解：
，
解不等式①，得x
；
解不等式②，得x≤3；
所以原不等式组的解集为：，
故答案为：．
18．解：方程组
，
由①得，y＝2﹣x③，
把③代入②得，x（2﹣x）＝﹣3，
解得：x1＝3，x2＝﹣1，
把x1＝3，x2＝﹣1分别代入③得，y1＝﹣1，y2＝3，
∴原方程组的解为：
或
．
故答案为：或．
19．解：两边平方得x﹣2＝9，解得x＝11，
经检验x＝11为原方程的解．
故答案为x＝11．
20．解：依据题意得x﹣4＝0或x+2＝0，
解得x＝4或x＝﹣2，
经检验x＝4为原方程的解．
故答案为x＝4．
三．解答卷（共8小题）
21．解：
，
解不等式①，得：x≤2，
解不等式②，得：x＞﹣1，
将不等式解集表示在数轴上如下：
所以不等式组的解集为﹣1＜x≤2．
22．解：两边乘（x+3）（x﹣3）得到：x（x﹣3）+6＝x+3
解得x1＝1，x2＝3，
经检验：x＝1是分式方程的解．
23．解：，
由①得：x＝y+2…③，
把③代入②并整理得：y2﹣2y﹣3＝0，
解这个方程得，y1＝3，y2＝﹣1，
把y的值分别代入③，得x1＝5，x2＝1．
∴原方程组的解为．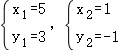
24．解：由①得：y＝3﹣x…③，
把③代入②得：x2+3x（3﹣x）+（3﹣x）2＝5，
整理得：x2﹣3x﹣4＝0，
解这个方程得，x1＝4，x2＝﹣1，
把x的值分别代入③，得y1＝﹣1，y2＝4．
∴原方程组的解为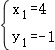
，．
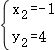25．解：去分母得：x（x+1）﹣6＝2x2+8x+6，
移项得：x2+x﹣6﹣2x2﹣8x﹣6＝0，
整理得：x2+7x+12＝0，即（x+3）（x+4）＝0，
解得：x1＝﹣3，x2＝﹣4，
经检验，x1＝﹣3是增根，舍去，
∴原方程的根是x＝﹣4．
26．解：去分母得：x﹣1+2＝x2﹣1，
整理得：x2﹣x﹣2＝0，即（x﹣2）（x+1）＝0，
解得 x＝﹣1或x＝2，
经检验：x＝﹣1是增根，舍去；
x＝2是原方程的根，
∴原方程的根是x＝2．
27．解：解不等式①，得：x＜3，
解不等式②，得：x≥﹣1，
则不等式组的解集为﹣1≤x＜3，
将不等式组的解集表示在数轴上如下：
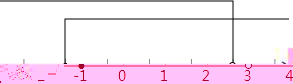
28．解：设科普类图书平均每本的价格是x元，则文学类图书平均每本的价格为（x﹣5）元，依据题意可得：
＝
﹣100，
解得：x＝20，
经检验得：x＝20是原方程的根，
答：科普类图书平均每本的价格是20元．
