2019-2020学年上海黄兴学校初中三年级（上）首次月考 数学试题
时间：90分钟 总分100分 2019.10
1、选择题：（本大题共6题，每题3分，满分18分）
1.在比率尺为1：500的地图上，量得甲、乙两地的距离为25cm，则甲乙两地的实质距离是 （ ）
A 1250km B 125km C 12.5km D 1.25km
2.下列命题中假命题的是 （ ）
A 各有一个角是45°的两个等腰三角形是相似三角形
B 各有一个角是60°的两个等腰三角形是相似三角形
C 各有一个角是105°的两个等腰三角形是相似三角形
D 两个等腰直角三角形是相似三角形
3.已知△ABC的三边长分别为
，
，2，△A’B’C’的两边长分别是1和
，假如△ABC与△A’B’C’相似，那样△A’B’C’的第三边长可以是 （ ）
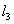A B 
C 
D 
如图，AB是斜靠在墙上的长梯，梯脚B距离墙角1.6m，梯上点D距墙1.4m，BD长0.55m，则梯子长为 （ ）
A 3.85m B 4.00m C 4.04m D 4.50m
直线DE交△ABC中的AB于D点，交AC于E点，那样能推出DE∥BC的条件是 （ ）
A B 
C 
D 
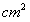如图把△ABC沿AB边平移到△DEF的地方，他们的重叠部分（即图中阴影部分）的面积是△ABC的面积的一半，若AB=，则此三角形移动的距离AD是（ ）
A 
B C 1 D 
2、填空题：（本大题共12题，每题3分，满分36分）
若
，则
的值等于__________；
已知线段
厘米，厘米，那样线段a和c的比率中项__________.
两个相似三角形的相似比为2:5，周长差为12厘米，则较大三角形的周长为__________.
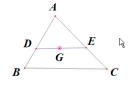
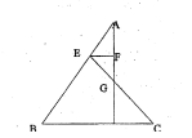
如图，在△ABC中，DE∥BC，DE过重心G，且分别与AB、AC交与点D、E，假如△ADE的面积为16,那样四边形BCED的面积为__________
已知线段AB的长是10㎝，点C是线段AB的黄金分割点且AC＜BC，则AC的长为__________㎝
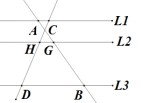
如图，
∥∥，已知AG=6㎝,BG=12㎝,CD=15㎝,CH=__________㎝
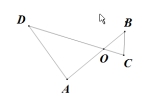
如图:AB、CD相交于O，且∠A=∠C，若OA=3,OD=4,OB=2,则OC=__________
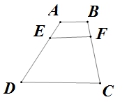
如图，AB∥EF∥CD,AB=2,CD=8,AE:ED=1:5,则EF的长度为__________
(第10题） （第12题） （第13题） （第14题）
如图，△ABC中边AB上有一点D，假如
,
,,则
__________
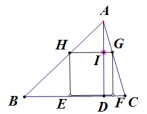
如图，四边形EFGH是△ABC内接正方形，BC=21㎝,高AD=15㎝，则内接正方形边长EF=__________
__________
（第15题） （第16题） （第17题） （第18题）
__________
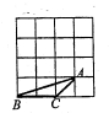
在网格中画出与△ABC一样的△
(相似比不为1）
如图，在平面直角坐标系中有两点A（4,0），B（0,2），假如点C在X轴上（C与A不重合），当点C的坐标为__________时，使得△BOC与△AOC相似
3、解答卷（19,20题各6分，21、22、23题各8分，24题10分，共46分）
如图，已知，AB∥FG，AC∥EH,BG=CH,求证：EF∥BC
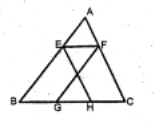
在△ABC中，点D、E分别边AB、AC上的点，若AD=2,DB=7,AE=3,EC=3,求DE:BC的值
如图，AD⊥于点D，点E在AB上，AD与CD交于点G，EF⊥AD于点F，AE=5㎝,BE=10㎝,CD=5㎝.求AF、GD的长.
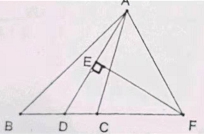
已知AD为∠BAC的角平分线，EF为AD的垂直平分线，求证：
如图，在正方形ABCD中，点F是边BC上一点（点F与点B、点C均不重合），AE⊥AF，AE交CD的延长线于点E，连接EF交AD于点G.
求证：
;
设正方形ABCD的边长为1，是不是存在这种点F，使得AF=FG？若存在，求出这个时候BF的长；若没有，请说明理由.
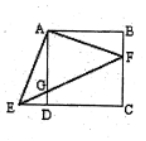
如图，已知在△ABC中，AB=AC=6,BC=5,D是AB上一点，BD=2,E是BC上一动点，联结DE，并作∠DEF=∠B,射线EF交线段AC于F.
求证：△DBE∽△ECF;
当F是线段AC的中点时，求线段BE的长；
联结DF，假如△DEF与△DBE相似，求FC的长.
__________
__________
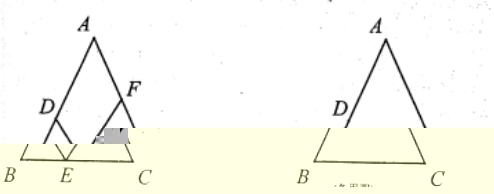
